ブログ
鵬雲賞授与式 卒業式予行練習
鵬雲賞授与式ならびに卒業式予行練習を行いました。
卒業式予行練習では、本番さながらの緊張感を持って臨むことができました。
給食でも節水対策が始まりました
節水の取り組みとして、本日からトレーの配膳がなくなりました…。
それぞれランチョンマット等を持参し、給食の時間を楽しんでいます!
個性が出ていていいですね!
2年生 進路オリエンテーションの様子
2年生総合の時間で、進路オリエンテーションを実施しました。
この時期は3年生の0学期とも呼ばれています。「受験・就職のスタートライン」へと意識を切り替えてほしいです。
2年 救命救急法
田原市消防署の方々にお越しいただき、救命救急法(2年生)を学びました。道具を用いて、心肺蘇生法やAEDの使用方法を習得することができました。
2年生高校説明会の様子
2年生総合の時間で、近隣の高等学校からお越しいただいた3校による高校説明会が行われました。
校風や生徒の雰囲気、在校生の生の声など、パンフレットだけでは分からない学校の「リアル」な姿を知ることができ、高校選びの重要な判断材料を得るための貴重な機会となりました。
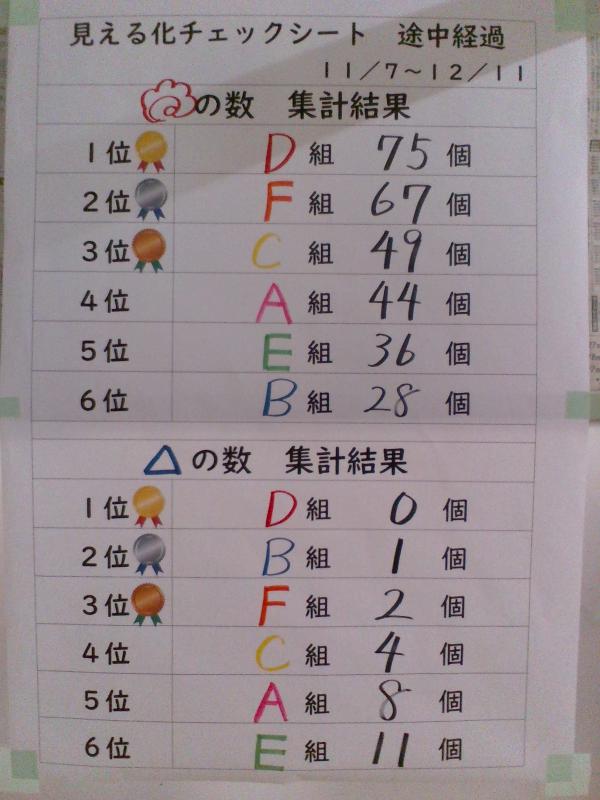
2年生 見える化計画
級長会で企画・実施している「見える化チェックシート」の途中経過です。
授業者がクラスとしての授業の取り組みを4段階で評価し、コメントを添え、その様子を「見える化」しました。
現在、合唱コンクールに引き続き、D組が1位!!!
「見える化」したことで、他クラスにも良い刺激になっているはず!
2学期も残り2週間を切りました…
後輩の手本になれる、より良い集団を目指しましょう!
2年生 生き方講演会②③
本日の総合の時間、2年生生き方講演会②③が行われました。
講師である太田健司様、清水阿子様から、「自分がやりたいこと」は何かを考えながら過ごすこと、生きることの大切さを学ぶことができました。
お二人の講師方、お忙しい中、ありがとうございました!
2年生 生き方講演会
本日の総合の時間、2年生生き方講演会が行われました。
講師である安田弦矢様から、仕事とは何か、今後の未来を予測しながら常にチャレンジしていくことの大切さや難しさを学ぶことができました。
今回の貴重な経験を、今後の生き方に活かしてください!
3年生理科 相手を落とせ!キャップファイター!
力学的エネルギーについての授業です。
多くの人が小学生のときに遊んだことがあるであろう、消しゴムを弾いて遊ぶゲームを、軽いペットボトルキャップと重いペットボトルキャップを用いて行いました。ゲームを通して、キャップの質量や弾き出す強さ(速さ)に注目し、エネルギーの大きさと関連づけて学習することができました。
2年生 国際交流
10/6(月) 10/7(金)
2年生英語科の授業でWorldClassroomを活用した国際交流を行いました。
2−A Indonesia
2−B Indonesia 
2−C Philippines 
2−D Malaysia 
2−E Indonesia 
2−F Indonesia 
フィリピンの先生と交流する男子生徒
生徒にとって非常に良い刺激になったと思います!
今回の貴重な経験を、今後の英語学習に活かしてください!